V dnešním videu se podíváme na několik základních a velmi užitečných finančních funkcí v Excelu, které vám pomohou během mžiku spočítat splátky, investice, úroky, hypotéku i úspory. Představíme si funkce SOUČHODNOTA, BUDHODNOTA, PLATBA, ÚROKOVÁ.MÍRA, POČET.OBDOBÍ a funkce PLATBA.ÚROK a PLATBA.ZÁKLAD. Jednotlivé finanční funkce si jako vždy ukážeme na praktických příkladech.
Excelový soubor ke stažení
Finanční funkce v Excelu
Všechny finanční funkce mají ve směs podobné parametry. Jsou jimi:
Sazba, což je úroková sazba, která je vztažená k danému období.
Parametr pper, což je doba, přičemž se většinou jedná o celkovou dobu splatnosti nebo délku investice.
Parametr splátka je výše splátky, která je vztažená k danému období.
Parametry Souč_hodnota a Bud_hodnota, což jsou parametry, které vyjadřují současnou a budoucí hodnotu.
Nepovinným parametrem je typ, kde máte většinou na výběr z polhůtního nebo předlhůtního úročení.
U finančních funkcí si musíte pamatovat to, že záleží na tom, zda současnou hodnotu, budoucí hodnotu a splátku vyplníte s mínusovým znaménkem. Výsledek finančních funkcí se totiž řídí z pohledu cashflow, tedy zda z našeho pohledu peníze přitékají nebo odtékají. V zásadě tak spořicí částky vycházejí s mínusovým znaménkem, jelikož se z pohledu toku financí jedná o výdaj. Úvěrové částky vycházejí s plusovým znaménkem, jelikož se z pohledu toku finanční jedná o příjem.
Vše si ale ukážeme na jednotlivých příkladech.
BUDHODNOTA / FV
Funkce BUDHODNOTA je zkratkou pro budoucí hodnotu. V angličtině se tato funkce jmenuje FV jako Future Value. Funkci Budoucí hodnota použijeme všude tam, kde nás zajímá budoucí hodnota investice nebo úvěru. Funkce BUDHODNOTA má následující tři povinné parametry. Sazba, což je úroková sazba, pper je celkové období a splátka, což je výše splátky. Následují dva nepovinné parametry současná hodnota a typ.
= BUDHODNOTA/FV (sazba; pper; splátka; [současná hodnota]; [typ])
Kolik naspoříme s počátečním vkladem?
Funkci BUDHODNOTA využijeme například tehdy, když nás zajímá, jaká bude budoucí hodnota naší investice. Řekněme, že máme 50 000 Kč (B3), které chceme uložit při 3 % ročním úroku (B4) na 5 let (B5). Zajímá nás, kolik peněz za těch 5 let naspoříme. V tomto případě nechceme již žádnou další částku měsíčně spořit navíc a úroky jsou na spořicí účet připisovány jednou ročně.
V buňce B7 využijeme funkci BUDHODNOTA, kde jako první parametr sazba vyplníme výši úroku. Úroky jsou připisovány jednou ročně, takže vyplníme roční úrokovou sazbu (B4). Dále máme parametr pper, tedy celkovou dobu, na kterou ukládáme peníze. To je 5 let (B5). Následuje výše splátky. Měsíční pravidelnou platbu v tomto příkladu nemáme, takže vyplníme nulu. Následuje parametr současná hodnota, což je v tomto případě hodnota počáteční investice. Jelikož spoříme, tak musíme současnou hodnotu vyplnit se znaménkem mínus (-B3). Posledním parametrem je typ. Máme na výběr Na konci období nebo Na začátku období, v praxi se jedná o předlhůtní nebo polhůtní připisování úroků. Řekněme, že v tomto příkladu nám spořicí účet připíše úroky vždy až na konci roku nebo období. Vyplníme proto nulu a funkci potvrdíme.
Vrátila se výše investice po pěti letech při zvolených parametrech.

Co kdyby ale úroky byly na spořicí účet připisovány měsíčně? Vedle v buňce C7 začneme znovu s funkcí BUDHODNOTA, kde jako sazbu znovu označíme roční úrokovou sazbu (B4), nicméně teď nám ji spořicí účet připisuje měsíčně, takže tuto sazbu musíme vydělit 12 (B4/12). Následuje parametr pper, což je doba investice nebo spoření, opět označíme celkovou dobu (B5), ale jelikož máme teď úrokovou sazbu převedenou na měsíce, tak musíme i celkovou dobu převést na měsíce, tím, že ji vynásobíme 12 (B5*12). Následuje parametr splátka. Měsíčně opět nic nespoříme, takže vyplníme nulu a současná hodnota je opět výše počáteční investice s mínusem (-B3).
Potvrdíme a vrátila se konečná hodnota investice, která je o něco málo vyšší než u ročního připisování úroků, což je způsobeno tím, že se úroky připisují měsíčně.

Kolik naspoříme s pravidelnou měsíční úložkou?
V dalším příkladu naopak nemáme počáteční investici, ale chceme měsíčně ukládat stále stejnou částku, řekněme 1 000 Kč. Tuto částku budeme ukládat na spořicí účet, kde máme úrok 3 % ročně a chceme tyto úložky provádět 5 let. Zajímá nás, kolik za těch 5 let naspoříme. Opět využijeme funkci BUDHODNOTA.
Jako parametr úrok vyplníme roční úrokovou sazbu, převedenou na měsíce (B14/12), jelikož úložky provádíme měsíčně a měsíčně se připisuje i úrok. Následuje celková doba spoření, převedená na měsíce (B15*12). Parametr splátka je tentokrát hodnota pravidelné měsíční investice, a jelikož se jedná o spoření, tak splátku uvedeme se znaménkem mínus (-B13). Současnou hodnotu, tedy počáteční investici, tentokrát nemáme, takže tento parametr přeskočíme. Pokud budeme peníze na spořicí účet ukládat na konci každého měsíce, tak vybereme nulu. Potvrdíme a funkce BUDHODNOTA vrátila částku, kterou za 5 let naspoříme.
Pokud by nás zajímalo, o kolik více bychom naspořili, kdybychom ukládali peníze vždy na začátku měsíce, tak v parametru Typ vyplníme jedničku.

Kolik naspoříme s počátečním vkladem a pravidelnou měsíční úložkou?
Počáteční investici a pravidelnou úložku můžeme i zkombinovat. Řekněme, že chceme na spořicí účet uložit 100 000 Kč a ještě pravidelně na tento účet chceme i spořit 2 500 Kč měsíčně. Zajímá nás kolik peněz naspoříme za 5 let.
Využijeme k tomu opět funkci BUDHODNOTA, kde jako úrokovou sazbu vyplníme roční úrok převedený na měsíční vyjádření (B25/12), pper je celková doba spoření převedená na měsíce (B26*12), výše splátky je hodnota měsíční investice s mínusem, jelikož se jedná o spoření (-B24). Současná hodnota je výše počáteční úložky s mínusem (-B23) a typ vyplníme nulu, jelikož peníze na účet posíláme na konci měsíce.
Potvrdíme funkci a vrátila se hodnota celkových úspor na konci 5 roku.

SOUČHODNOTA / PV
Funkce SOUČHODNOTA, anglicky funkce PV, jako Present Value, nám dovoluje určit současnou hodnotu budoucí investice nebo půjčky. Zjednodušeně ji tedy využijeme tam, kde nás zajímá, jakou hodnotu má dnes nějaká budoucí částka, a to při stejné úrokové sazbě. Funkce SOUČHODNOTA má tři povinné parametry, jsou jimi sazba, období pper a splátka. Nepovinnými parametry jsou budoucí hodnota a typ.
= SOUČHODNOTA/PV (sazba; pper; splátka; [budoucí hodnota]; [typ])
Kolik musíme dnes uložit abychom naspořili cílovou částku?
Funkci SOUČHODNOTA využijeme například tehdy, pokud nás zajímá, kolik bychom dnes museli uložit na spořicí účet, pokud bychom chtěli mít za 15 let naspořeno 1 mil. Kč.
Do buňky B38 napíšeme funkci SOUČHODNOTA, kde jako sazbu vyplníme roční úrokovou sazbu (B35), v tomto příkladu nám opět úroky připisují jednou ročně, takže sazbu nemusíme převádět na měsíční vyjádření. Následuje období, což je 15 let (B36). Parametr splátka nemáme, jelikož měsíčně nic nespoříme (0) a budoucí hodnota je milion korun, který hodláme naspořit (B34). Typ necháme základní, tedy že se úroky připisují na konci období. Funkci potvrdíme.
Abychom za 15 let při 3 % sazbě naspořili milion korun, tak bychom dnes na tento spořicí účet museli uložit částku 641 tisíc korun. Částka 641 tisíc korun je záporná, jelikož z našeho pohledu se jedná o výdaj. Pokud byste nechtěli mít tuto částku s mínusem, tak můžete před celou funkci SOUČHODNOTA napsat mínus a nebo mínus napsat před budoucí hodnotu ve funkci, tak jako na obrázku č.5.

Jaký maximální úvěr si můžeme vzít?
Funkci SOUČHODNOTA využijete i výpočtu úvěrů. V dalším příkladu nás zajímá, jaký maximální úvěr si můžeme vzít, pokud můžeme měsíčně splácet 5 000 Kč. Do buňky B48 napíšeme funkci SOUČHODNOTA, kde jako sazbu vyplníme roční úrok (B45), ale jelikož budeme splácet měsíčně, tak tuto sazbu převedeme na měsíční vyjádření (B45/12). Následuje období, tedy doba na kterou bychom si úrok vzali, převedený na měsíce (B46*12). A splátka je výše maximální měsíční splátky, kterou můžeme splácet (B44). A jelikož nechceme mít výslednou částku s mínusem, tak rovnou před celou funkci SOUČHODNOTA napíšeme mínus a funkci potvrdíme.
A máme maximální výši úvěru, kterou si při zadaných parametrech můžeme půjčit.

POČET.OBDOBÍ / NPER
Na dalším příkladu si ukážeme funkci POČET.OBDOBÍ, anglicky funkci NPER. Jedná se o funkci, která spočítá při zadaných parametrech počet období. Ve funkci POČET.OBDOBÍ máme jako první povinný parametr sazbu, druhým parametrem je místo období parametr splátka a následuje současná hodnota. Nepovinnými parametry jsou budoucí hodnota a typ.
= POČET.OBDOBÍ/NPER (sazba; splátka; současná hodnota;[budoucí hodnota]; [typ])
Za jak dlouho naspoříme cílovou částku?
V tomto příkladu nás zajímá, za jak dlouho naspoříme 1 mil. Kč. Do buňky B59 vyplníme funkci POČET.OBDOBÍ, kde jako sazbu označíme úrokovou sazbu převedenou na měsíční vyjádření (B57/12). Následuje výše měsíční splátky s mínusem (-B56) a současná hodnota, což je výše počátečního vkladu, pokud tuto hodnotu máme, opět s mínusem (-B55). Jako nepovinný parametr budoucí hodnota vyplníme částku, kterou plánujeme naspořit, tedy 1 mil. Kč (B54). Funkci potvrdíme.
Vrátil se počet měsíců, za kterou cílovou částku naspoříme. Pokud bychom chtěli toto číslo v letech, tak celou funkci vydělíme číslem 12.

PLATBA / PMT
Další užitečnou finanční funkcí je funkce PLATBA, v anglické verzi Excelu funkce PMT. Tato funkce vám dovoluje spočítat platbu a to buď u úvěru i hypotéky nebo spoření. Povinnými parametry funkce PLATBA jsou sazba, parametr pper a současná hodnota. Nepovinnými parametry jsou budoucí hodnota a typ.
= PLATBA/PMT (sazba; pper; současná hodnota;[budoucí hodnota]; [typ])
Kolik musíme měsíčně ukládat abychom naspořili cílovou částku?
V tomto příkladu nás zajímá, kolik bychom měsíčně měli spořit, abychom naspořili za 20 let milion korun, při dané úrokové sazbě.
V buňce B69 využijeme funkci PLATBA. Prvním povinným parametrem funkce PLATBA je sazba, tedy úroková sazba a jelikož spoříme měsíčně, tak sazbu vydělíme číslem 12 (B66/12). Následuje opět období tedy parametr pper, tedy počet let vynásobený číslem 12 (B67*12). Posledním povinným parametrem je současná hodnota, kterou v tomto příkladu nemáme. My máme stanovenou budoucí hodnotu, kterou chceme naspořit. Takže parametr současná hodnota přeskočíme a vyplníme parametr budoucí hodnota s mínusem (-B65), abychom výslednou částku měli jako kladné číslo.
Funkci potvrdíme a vrátila se výše měsíční úložky, kterou musíme spořit abychom naspořili 1 mil. Kč.

ÚROKOVÁ.MÍRA / RATE
Finanční funkce, která vám dovoluje spočítat úrokovou sazbu je funkce ÚROKOVÁ.MÍRA, anglicky funkce RATE. Stejně jako ostatní finanční funkce má i tato funkce jako povinné parametry pper, splátku a současnou hodnotu. Nepovinnými parametry jsou budoucí hodnota, typ a odhad.
= ÚROKOVÁ.MÍRA/RATE (pper; splátka; současná hodnota;[budoucí hodnota]; [typ]; [odhad])
Za jakou úrokovou sazbu musíme peníze uložit, abychom naspořili cílovou částku?
Řekněme, že chceme zjistit, za jakou úrokovou sazbu bychom museli uložit sto tisíc korun, abychom za 20 let naspořili milion, když k tomu budeme ještě měsíčně spořit 2 500 Kč.
Stejně jako u ostatních finančních funkcí jsou i zde povinné parametry velmi podobné. Do buňky B80 napíšeme funkci ÚROKOVÁ.MÍRA, kde prvním povinným parametrem je období. Vyplníme tedy počet let (B77). Následuje splátka a jelikož chceme celé vyjádření na roční bázi tak vyplníme měsíční úložku s mínusem a vynásobíme ji 12 (-B75*12). Následuje parametr současná hodnota, což je výše počátečního vkladu s mínusem (-B76) a budoucí hodnota je cílová částka, tedy milion korun (B78).
Funkci potvrdíme a vyšla nám roční úroková sazba, za kterou musíme peníze uložit, abychom naspořili cílovou částku.

Poměr úroků a jistiny v anuitní splátce
Nakonec si ještě ukážeme dvě dodatečné funkce, které doplňují funkci PLATBA. Jedná se o funkce PLATBA.ÚROK a PLATBA.ZÁKLAD. Něco málo o těchto funkcích jsme si již ukázali ve videu na Akademii Excelu Jak vytvořit hypoteční kalkulačku. Velmi často se tak tyto funkce používají jako doplněk funkce PLATBA u výpočtu hypotečních splátek.
Na výpočtu hypotečního úvěru si ukážeme i tyto funkce. Zadání příkladu je velmi jednoduché. Výše hypotečního úvěru je 5 mil. Kč, přičemž zde máme uvedou i úrokovou sazbu a celkovou dobu splatnosti. Naším úkolem je nejprve spočítat výši celkové splátky úvěru a následně dopočítat, jaký podíl na splátce tvoří úroky a jaký jistina.
Začneme funkcí PLATBA, pomocí které spočítáme celkovou výši splátky.
Do buňky B90 napíšeme funkci PLATBA, kde jako sazbu označíme roční úrokovou sazbu (B87/12), jelikož nás ale zajímá měsíční splátka hypotéky, tak tuto sazbu vydělíme 12. Následuje parametr pper, což je celková doba splatnosti, označíme tedy celkovou dobu v letech, ale opět musíme tento parametr vztáhnout k měsíční periodě, takže počet let vynásobíme dvanácti (B88*12). Současná hodnota je výše úvěru, a jelikož nechceme celkovou splátku s mínusem, tak před současnou hodnotu napíšeme mínus (-B86).
Funkci potvrdíme a vrátila se výše měsíční splátky hypotéky při zadaných parametrech.
V každé anuitní splátce je ovšem určitý podíl úroků a jistiny.

PLATBA.ÚROK / IPMT
Funkce PLATBA.ÚROK v angličtině funkce IPMT, jako interest payment, se používá pro výpočet výše úroků v anuitní splátce. Funkce PLATBA.ÚROK má jako povinné parametry sazbu, parametr za, parametr pper a současnou hodnotu. Nepovinnými parametry jsou budoucí hodnota a typ.
=PLATBA.ÚROK (sazba; za; pper; souč_hodnota; [bud_hodnota]; [typ])
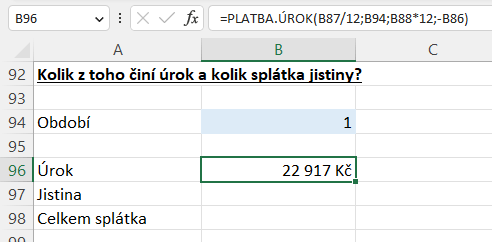
Do buňky B96 napíšeme funkci PLATBA.ÚROK, kde nejprve označíme výši úrokové sazby, a opět musíme i v tomto výpočtu převést roční vyjádření na měsíční, takže sazbu vydělíme dvanácti (B87/12). Parametr za je období, pro které chceme výši úroků spočítat. Nacházíme se na počátku úvěru, takže nás zajímá poměr pro první měsíc. Tento parametr máme vyjádřený v buňce B94, takže označíme tuto buňku. Následuje parametr pper, což je opět celková doba splatnosti vynásobená dvanácti (B88*12). Současná hodnota je celková výše úvěru s mínusem (-B86).
Funkci potvrdíme a vrátila se výše úroků ve splátce úvěru v prvním měsíci splácení úvěru.
PLATBA.ZÁKLAD / PPMT
Funkce PLATBA.ZÁKLAD, anglicky funkce PPMT se zase používá pro výpočet výše jistiny v anuitní splátce. Parametry funkce jsou totožné jako u funkce PLATBA.ÚROK.
= PLATBA.ZÁKLAD (sazba; za; pper; souč_hodnota; [bud_hodnota]; [typ])
V buňce B97 nejprve označíme výši úrokové sazby převedenou na měsíce (B87/12). Parametr za je opět jednička, tedy buňka B94. Následuje parametr pper, což je opět celková doba splatnosti vynásobená dvanácti (B88*12). Současná hodnota je celková výše úvěru s mínusem (-B86). Funkci potvrdíme a vrátila se výše úmoru ve splátce úvěru v prvním měsíci splácení úvěru.

Jelikož funkce pro výpočet úroků a úmoru počítají poměr ve funkci PLATBA, tak se součet těchto funkcí musí rovnat výsledku funkce PLATBA. Tedy že součet úroku a úmoru je roven výši splátky. Součet hodnot v buňce B98 se rovná hodnotě funkce PLATBA v buňce B90.

Pokud by nás zajímal poměr úroků a jistiny například na konci druhého roku splácení, tedy ve 24 měsíci, tak do buňky B94 (do parametru za) napíšeme místo jedničky číslo 24, což je 24. měsíc. A funkce se přepočítají.





